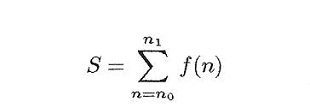
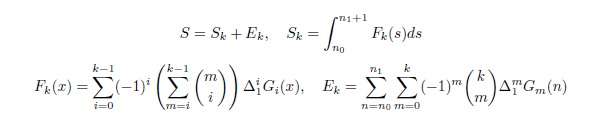
En el campo de las matemáticas se suele denominar una serie a una suma de finitos o infinitos términos, los cuales responden a una fórmula de la que se extrae cada valor particular de cada término de la suma. En realidad existen otras conceptualizaciones que responden a la palabra «serie». Por ejemplo, podemos tener una serie de composición de grupos de un grupo dado G, donde cada subgrupo constituyente es un subgrupo normal del inmediatamente siguiente; pero esto es ya algo totalmente diferente a lo que primero enuncié, tiene que ver con la teoría de grupos. Hablando estrictamente de series en el sentido de sumas de números, un problema que aparece de forma natural, y del que es deseable una solución o al menos una aproximación, es el cálculo de la adición de la serie. Sumar números con un computador no es difícil, basta desarrollar un programa de cálculo, que puede ser muy sencillo, dependiendo del lenguaje de programación empleado. Pero las matemáticas son muy rigurosas, es la forma de razonamiento tal vez más exigente, puesto que ha de haber una pulcritud e irrefutabilidad aplastantes en las demostraciones. La intuición que tan bien funciona en un juicio o en la investigación criminal, unida a las pruebas, aquí sólo sirve -y es mucho ésto- para establecer el punto de partida y para ver la forma de solucionar el problema, antes de demostrarlo, lo que realmente vale es la demostración irrefutable. Los matemáticos -los de verdad, yo sólo soy un aficionado de los malos- convierten café en teoremas (como dijo Paul Erdös), y sus creaciones pueden llegar a ser de una belleza estremecedora -dependiendo también del ojo que la observa-. Al que le pueda interesar, aquí dejo un método que he desarrollado para sumar series, que está convenientemente registrado en el Registro de la Propiedad Intelectual con mi nombre y apellidos. La idea subyacente consiste en identificar una serie con la integral de Lebesgue del histograma de barras de anchura unidad y altura igual a la particularización de la función sumada a los números naturales. Si extendemos esta función al dominio de los reales y calculamos su integral de Lebesgue en el intervalo de sumación, ésta resulta ser igual a la serie buscada más un exceso de área hasta cubrir dicha extensión. Este exceso de área se puede interpretar como otra serie. De este modo, podemos seguir iterando indefinidamente, o al menos hasta una iteración en la que el error esperado es menor que un valor dado.
PARA INICIAR LA DESCARGA CLICAR AQUÍ : metodo_expansion_integral